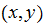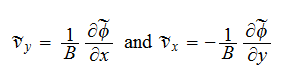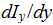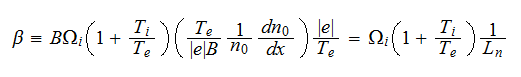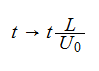Slab model for the ion mode and the barotropic equation
Florin Cadarache and Magurele
Abstract:This part introduces a simple model for the nonlinear ion mode and shows that it is possible to reduce it to the barotropic equation.
The
slab model of the ion mode instability
We consider cylindrical geometry with circular magnetic surfaces. Locally the
model can be reduced to a slab geometry with
 cartezian coordinates replacing respectively the radius and poloidal angle
coordinates
cartezian coordinates replacing respectively the radius and poloidal angle
coordinates
 .
At equilibrium the plasma parameters are constant on the magnetic surfaces.
The effects of the toroidicity and of the particle drifts are not included
instead the nonlinearity related to the ion polarization drift is fully
retained. The plasma model consists of the continuity equations and the
equations of motion for electrons and ions:
.
At equilibrium the plasma parameters are constant on the magnetic surfaces.
The effects of the toroidicity and of the particle drifts are not included
instead the nonlinearity related to the ion polarization drift is fully
retained. The plasma model consists of the continuity equations and the
equations of motion for electrons and ions:

 where
where
 .
The friction forces
.
The friction forces
 , which are important for the parallel electron momentum balance, vanish for
infinite plasma conductivity, which we will assume. The collisional viscosity
, which are important for the parallel electron momentum balance, vanish for
infinite plasma conductivity, which we will assume. The collisional viscosity
 will be neglected as well. However we will need to include it later when we
will consider the balance of the forces contributing to the poloidal rotation.
The electron and ion temperatures are considered constant along the magnetic
lines
will be neglected as well. However we will need to include it later when we
will consider the balance of the forces contributing to the poloidal rotation.
The electron and ion temperatures are considered constant along the magnetic
lines
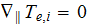 .
The equilibrium quantities are perturbed by the wave potential
.
The equilibrium quantities are perturbed by the wave potential
 :
:
 .
A sheared poloidal plasma rotation is included, and we later will make
explicit the corresponding part in the potential,
.
A sheared poloidal plasma rotation is included, and we later will make
explicit the corresponding part in the potential,
 .
.
The momentum conservation equations are used to determine the perpendicular
velocities of the electrons and ions. The parallel momentum conservation
equation for electrons, in the absence of dissipation or
drifts gives the adiabatic distribution of the density fluctuation.
The velocities are introduced in the continuity equations to find the
dynamical equations for the density and electric potential.
From the equations of motion for the ions the velocities are obtained
in the form:
 where the ion diamagnetic velocity is
where the ion diamagnetic velocity is
 The versor of the magnetic field is
The versor of the magnetic field is
 ;
the versors along the transversal coordinate axis
;
the versors along the transversal coordinate axis
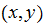 will be noted
will be noted
 .
The ion-polarization velocity is:
.
The ion-polarization velocity is:
 Using the notation
Using the notation
 the perpendicular ion velocity can be written
the perpendicular ion velocity can be written

The equation for the velocity of the electrons is


We assume neutrality
 and introduce the expressions of the velocities in the continuity equations
for ions and for electrons.
and introduce the expressions of the velocities in the continuity equations
for ions and for electrons.
The ion continuity equation is

The electron continuity equation is
 The equations are substracted , to obtain
The equations are substracted , to obtain
 From the last term in the left we get:
From the last term in the left we get:
 Including the similar term for the electrons, we obtain
Including the similar term for the electrons, we obtain
 or:
or:
 From the continuity equation for electrons
From the continuity equation for electrons
 we obtain
we obtain
 where the seed poloidal velocity is
where the seed poloidal velocity is
 .
The parallel momenttum balance gives the parallel electron velocity
.
The parallel momenttum balance gives the parallel electron velocity
 In the absence of friction
In the absence of friction
 and of particle drifts the electron response is adiabatic
and of particle drifts the electron response is adiabatic
 and the potential is determined from Eq.(eq2). To
develop separately the ion-polarization drift term, we introduce the notation:
and the potential is determined from Eq.(eq2). To
develop separately the ion-polarization drift term, we introduce the notation:
 where we make explicit the electric potential
where we make explicit the electric potential
 associated to the initial plasma poloidal rotation,
associated to the initial plasma poloidal rotation,
 .
.
 We have
We have
 or
or
 with the relations
with the relations

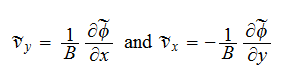 After very simple calculations we obtain:
After very simple calculations we obtain:
 and
and
 It will be useful to calculate the derivaties of these quantities
It will be useful to calculate the derivaties of these quantities
 and
and

The quantity denoted by
 takes the form
takes the form

The mode evolution in a fixed
plasma rotation profile
We will assume that the mode evolves initially without perturbing the
equilibrium profiles, in particular the seed poloidal rotation. This allows us
to simplify the expressions above, taking:
 Then the first lines in the formulas Eqs.(ir),
(didr), (didy) are zero. Let
us consider in the expression of
Then the first lines in the formulas Eqs.(ir),
(didr), (didy) are zero. Let
us consider in the expression of
 the part
the part
 which does not contain the fluctuating density
which does not contain the fluctuating density
 .
Writting
.
Writting
 we have
we have
 and
and
 Replacing the perturbed velocity by the perturbed potential, writting all
terms and summing, we get:
Replacing the perturbed velocity by the perturbed potential, writting all
terms and summing, we get:
 Collecting all what we have at this moment the ion continuity equation
(eq2) becomes:
Collecting all what we have at this moment the ion continuity equation
(eq2) becomes:

In the above equation (which is exact) we shall make the following
approximations:
The resulting equation is
 and, replace the adiabatic form of the density perturbation
and, replace the adiabatic form of the density perturbation
 We define
We define
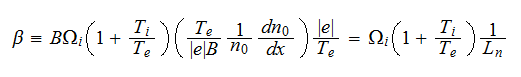 and obtain
and obtain
 which is the barotropic equation.
which is the barotropic equation.
Nondimensional form of the equation
We consider that the ion mode extends in the spatial
( )
direction over a length
)
direction over a length
 .
A typical value for the sheared poloidal rotation is noted
.
A typical value for the sheared poloidal rotation is noted
 .
We make the replacements
.
We make the replacements

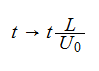

 such that from now on
such that from now on
 and
and
 are nondimensional quantities. We also change the radial coordinate into a
dimensionless variable
are nondimensional quantities. We also change the radial coordinate into a
dimensionless variable
 and rewrite the equation
and rewrite the equation
 The coefficients are
The coefficients are


For an order of magnitude,
 is the ratio of the diamagnetic electron velocity to the rotation velocity
is the ratio of the diamagnetic electron velocity to the rotation velocity
 multiplied by the ratio of the density gradient length to the length of the
spatial domain. This quantity,
multiplied by the ratio of the density gradient length to the length of the
spatial domain. This quantity,
 is in general smaller than unity.
is in general smaller than unity.
The quantity
 is the ratio of the ion cyclotron frequency to the inverse of the time
required to cross the spatial domain with the typical flow velocity. Since the
later
is the ratio of the ion cyclotron frequency to the inverse of the time
required to cross the spatial domain with the typical flow velocity. Since the
later
 involves macroscopic quantities this ratio can be large. It is multiplied by
the ratio of the spatial length to the density gradient length (these
quantities can be comparable and the ratio not too different of unity).
involves macroscopic quantities this ratio can be large. It is multiplied by
the ratio of the spatial length to the density gradient length (these
quantities can be comparable and the ratio not too different of unity).
We change the notations eliminating the primes. The equation becomes

This is the barotropic equation, known in the physics of the
atmosphere.
 cartezian coordinates replacing respectively the radius and poloidal angle
coordinates
cartezian coordinates replacing respectively the radius and poloidal angle
coordinates
 .
At equilibrium the plasma parameters are constant on the magnetic surfaces.
The effects of the toroidicity and of the particle drifts are not included
instead the nonlinearity related to the ion polarization drift is fully
retained. The plasma model consists of the continuity equations and the
equations of motion for electrons and ions:
.
At equilibrium the plasma parameters are constant on the magnetic surfaces.
The effects of the toroidicity and of the particle drifts are not included
instead the nonlinearity related to the ion polarization drift is fully
retained. The plasma model consists of the continuity equations and the
equations of motion for electrons and ions:

 where
where
 .
The friction forces
.
The friction forces
 , which are important for the parallel electron momentum balance, vanish for
infinite plasma conductivity, which we will assume. The collisional viscosity
, which are important for the parallel electron momentum balance, vanish for
infinite plasma conductivity, which we will assume. The collisional viscosity
 will be neglected as well. However we will need to include it later when we
will consider the balance of the forces contributing to the poloidal rotation.
The electron and ion temperatures are considered constant along the magnetic
lines
will be neglected as well. However we will need to include it later when we
will consider the balance of the forces contributing to the poloidal rotation.
The electron and ion temperatures are considered constant along the magnetic
lines
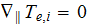 .
The equilibrium quantities are perturbed by the wave potential
.
The equilibrium quantities are perturbed by the wave potential
 :
:
 .
A sheared poloidal plasma rotation is included, and we later will make
explicit the corresponding part in the potential,
.
A sheared poloidal plasma rotation is included, and we later will make
explicit the corresponding part in the potential,
 .
.